cuestionario geometría

hola, os pongo AQUÍ cuestionario de geometría de hoy, no olvidéis de poner vuestro correo electrónico, nombre y apellidos y darle al final al botón enviar.

CLASES TELEMÁTICAS DE 3º ESO (LA FUNCIÓN RECTA)

Hola, os pongo un padlet con la información relativa a lo que tendríamos que dar esta semana en clase, la función recta. El primer documento es la teoría, que la tenéis en el libro y el resto son vídeos explicativos

problemas relativos a funciones y sus gráficas

Hola, os pongo un pdf sobre gráficas de funciones contextualizadas en situaciones de la vida diaria. Lo vemos en clase con el proyector pero podéis descargarlo o verlo pinchando AQUÍ.

Ficha de repaso global

Hola, aquí tenéis la ficha de repaso del global de álgebra. Tienen la solución. Pero eso no quiere decir que salgan en el examen. Sirve de repaso en casa. Pincha AQUÍ.

LA FICHA DE POLINOMIOS CON SOLUCIONES

Hola, para todos aquellos que queráis comprobar si habéis hecho bien los ejercicios de polinomios os pongo este enlace para que os descarguéis la ficha con las soluciones.

AQUÍ

REPASO ANTES DEL GLOBAL

Hola, como hemos visto en clase, el examen global será de los temas 1, 2 y 3.
Los estándares más importantes son:
a) Hallar fracción generatriz
b) Operar fracciones y resolver problemas de fracciones
c) Aproximación por truncamiento y redondeo. Errores absoluto y relativo
c) Operar potencias todo tipo
d) Operar en notación científica
e) Operar con raíces de cualquier índice
f) Hallar términos de una sucesión dado su término general
g) Hallar a1, d, an en una progresión aritmética
h) hallar a1, r, an en una progresión geométrica
i) Hallar la suma de n términos o infinitos términos
j) Problemas de interés compuesto anual.

Pincha en cada palabra clave para ir a una página web con ejercicios resueltos para practicar

LAS SUCESIONES POR RECURRENCIA, LA SUCESIÓN DE FIBONACCI, LA RAZÓN ÁUREA Y LA PRESENCIA DE ESTAS SUCESIONES EN LA NATURALEZA Y LAS ARTES

Hola, como vimos en clase hay unas sucesiones llamadas recurrentes que se obtienen dados los dos primeros términos el siguiente se obtiene con la suma de los dos anteriores

an+2 = a n+1 +a n


La sucesión más antigua y más conocida es la sucesión de Fibonacci, A={0. 1. 1. 2. 3. 5. 8. 13. 21. ...}, que conlleva un problema planteado por Fibonacci. El problema dice así: ¿Cuántas parejas de conejos tendremos a fin de año, si comenzamos con una pareja que produce cada mes otra pareja que procrea a su vez a los dos meses de vida?



Tras un número muy grande de términos, el cociente entre el último y el penúltimo término tiende a un número irracional llamado Razón áurea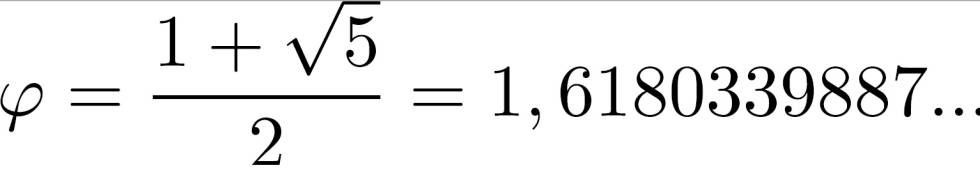 

Es un número especial que se encuentra al dividir una línea en dos partes, de modo que la parte más larga (a) dividida por la parte más pequeña (b) es igual a la longitud total dividida por la parte más larga.

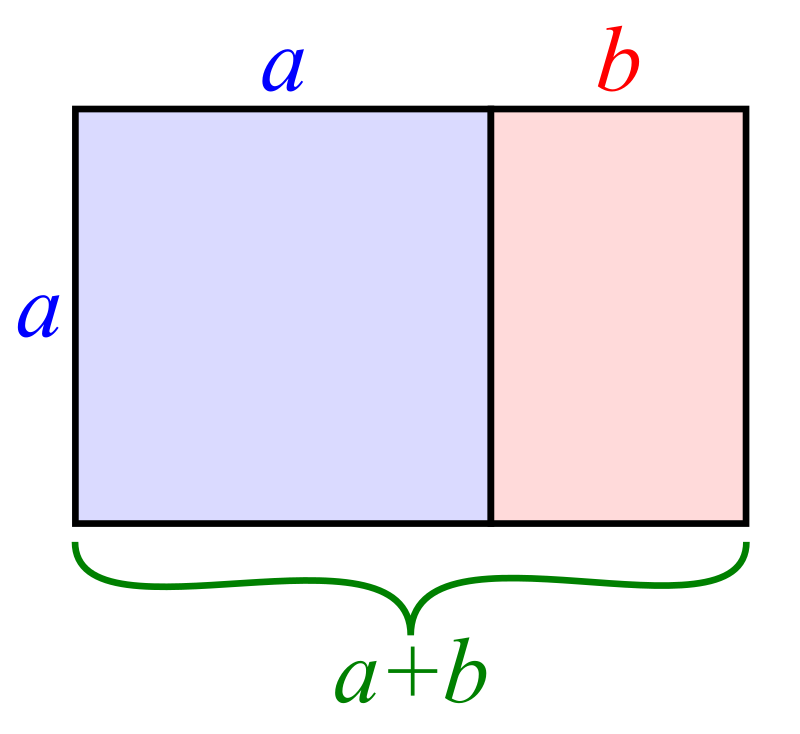
Eso dio lugar a crear con esas dimensiones rectángulos armoniosos, presentes en muchas obras de arte y en muchas medidas en la naturaleza (por ejemplo relaciones entre partes consecutivas del cuerpo humano, etc...),   

Los números de la sucesión de Fibonacci consiguen crear en cada paso un rectángulo áureo.

Además si creamos con arcos de circunferencia con los rectángulos formados obtenemos una espiral áurea, también presente en muchos aspectos de la naturaleza. 





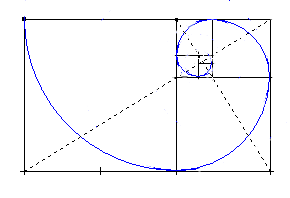
El trabajo de investigación que tenéis que hacer es encontrar 1 ejemplo de la naturaleza o el arte donde se recreen estos números de Fibonacci, o las razones áureas o rectángulos áureos o espirales áureas. Buscáis imágenes que lo muestren y lo guardáis en un archivo de texto con vuestro nombre y apellidos, el curso donde estáis, añadiendo la palabra Fibonacci y lo mandáis al siguiente correo

matesinstitutolamanga@gmail.com 

Este trabajo es independiente de los exámenes y es una nota que se suma a la nota final de curso con un peso de 0.2 %, o sea 0.02 puntos a añadir a la nota final. Esperamos vuestros trabajos de investigación. Fecha límite 13 de diciembre de 2019