Hola, como hemos visto en clase, el examen global será de los temas 1, 2 y 3.
Los estándares más importantes son:
a) Hallar fracción generatriz
b) Operar fracciones y resolver problemas de fracciones
c) Aproximación por truncamiento y redondeo. Errores absoluto y relativo
c) Operar potencias todo tipo
d) Operar en notación científica
e) Operar con raíces de cualquier índice
f) Hallar términos de una sucesión dado su término general
g) Hallar a1, d, an en una progresión aritmética
h) hallar a1, r, an en una progresión geométrica
i) Hallar la suma de n términos o infinitos términos
j) Problemas de interés compuesto anual.
Pincha en cada palabra clave para ir a una página web con ejercicios resueltos para practicar
viernes, 29 de noviembre de 2019
martes, 26 de noviembre de 2019
LAS SUCESIONES POR RECURRENCIA, LA SUCESIÓN DE FIBONACCI, LA RAZÓN ÁUREA Y LA PRESENCIA DE ESTAS SUCESIONES EN LA NATURALEZA Y LAS ARTES
Hola, como vimos en clase hay unas sucesiones llamadas recurrentes que se obtienen dados los dos primeros términos el siguiente se obtiene con la suma de los dos anteriores
an+2 = a n+1 +a n
La sucesión más antigua y más conocida es la sucesión de Fibonacci, A={0. 1. 1. 2. 3. 5. 8. 13. 21. ...}, que conlleva un problema planteado por Fibonacci. El problema dice así: ¿Cuántas parejas de conejos tendremos a fin de año, si comenzamos con una pareja que produce cada mes otra pareja que procrea a su vez a los dos meses de vida?

Tras un número muy grande de términos, el cociente entre el último y el penúltimo término tiende a un número irracional llamado Razón áurea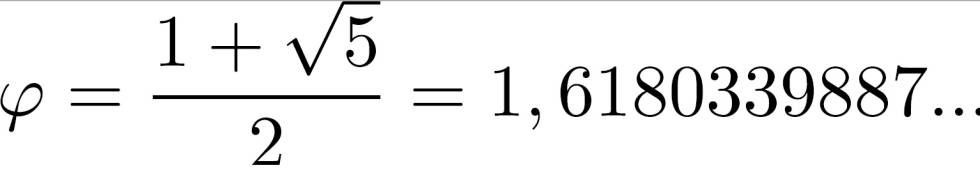
Es un número especial que se encuentra al dividir una línea en dos partes, de modo que la parte más larga (a) dividida por la parte más pequeña (b) es igual a la longitud total dividida por la parte más larga.
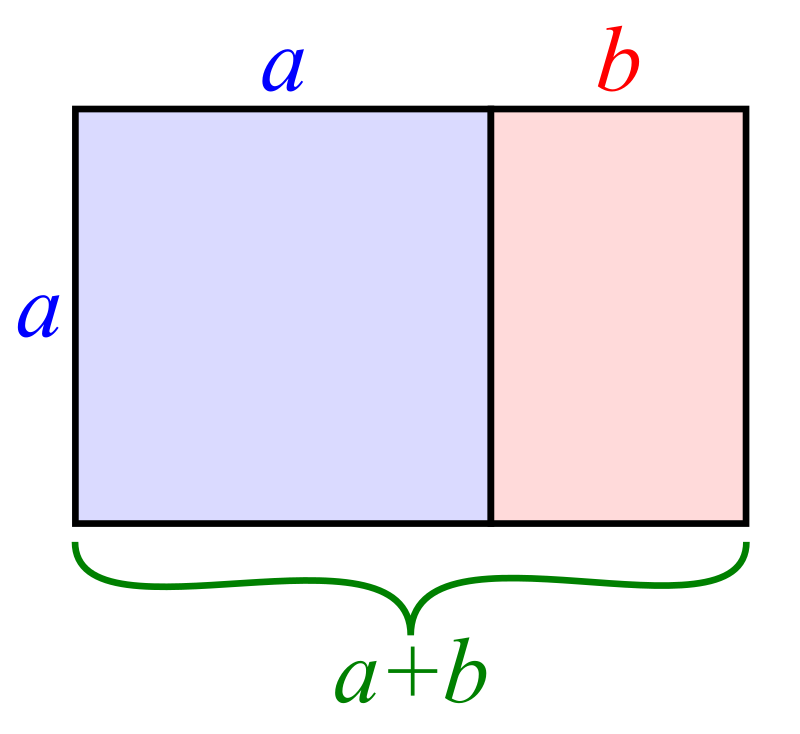

Eso dio lugar a crear con esas dimensiones rectángulos armoniosos, presentes en muchas obras de arte y en muchas medidas en la naturaleza (por ejemplo relaciones entre partes consecutivas del cuerpo humano, etc...),
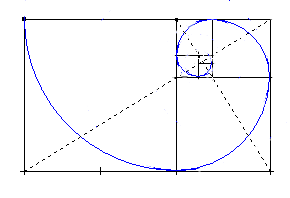
Los números de la sucesión de Fibonacci consiguen crear en cada paso un rectángulo áureo.
Además si creamos con arcos de circunferencia con los rectángulos formados obtenemos una espiral áurea, también presente en muchos aspectos de la naturaleza.
El trabajo de investigación que tenéis que hacer es encontrar 1 ejemplo de la naturaleza o el arte donde se recreen estos números de Fibonacci, o las razones áureas o rectángulos áureos o espirales áureas. Buscáis imágenes que lo muestren y lo guardáis en un archivo de texto con vuestro nombre y apellidos, el curso donde estáis, añadiendo la palabra Fibonacci y lo mandáis al siguiente correo
matesinstitutolamanga@gmail.com
Este trabajo es independiente de los exámenes y es una nota que se suma a la nota final de curso con un peso de 0.2 %, o sea 0.02 puntos a añadir a la nota final. Esperamos vuestros trabajos de investigación. Fecha límite 13 de diciembre de 2019
an+2 = a n+1 +a n
La sucesión más antigua y más conocida es la sucesión de Fibonacci, A={0. 1. 1. 2. 3. 5. 8. 13. 21. ...}, que conlleva un problema planteado por Fibonacci. El problema dice así: ¿Cuántas parejas de conejos tendremos a fin de año, si comenzamos con una pareja que produce cada mes otra pareja que procrea a su vez a los dos meses de vida?

Tras un número muy grande de términos, el cociente entre el último y el penúltimo término tiende a un número irracional llamado Razón áurea
Es un número especial que se encuentra al dividir una línea en dos partes, de modo que la parte más larga (a) dividida por la parte más pequeña (b) es igual a la longitud total dividida por la parte más larga.


Eso dio lugar a crear con esas dimensiones rectángulos armoniosos, presentes en muchas obras de arte y en muchas medidas en la naturaleza (por ejemplo relaciones entre partes consecutivas del cuerpo humano, etc...),
Los números de la sucesión de Fibonacci consiguen crear en cada paso un rectángulo áureo.
Además si creamos con arcos de circunferencia con los rectángulos formados obtenemos una espiral áurea, también presente en muchos aspectos de la naturaleza.

El trabajo de investigación que tenéis que hacer es encontrar 1 ejemplo de la naturaleza o el arte donde se recreen estos números de Fibonacci, o las razones áureas o rectángulos áureos o espirales áureas. Buscáis imágenes que lo muestren y lo guardáis en un archivo de texto con vuestro nombre y apellidos, el curso donde estáis, añadiendo la palabra Fibonacci y lo mandáis al siguiente correo
matesinstitutolamanga@gmail.com
Este trabajo es independiente de los exámenes y es una nota que se suma a la nota final de curso con un peso de 0.2 %, o sea 0.02 puntos a añadir a la nota final. Esperamos vuestros trabajos de investigación. Fecha límite 13 de diciembre de 2019
APLICACIONES DE LAS PROGRESIONES
Una de las aplicaciones de las progresiones es el interés compuesto bancario. Cuando uno ingresa dinero en el banco, si el dinero no se retira, se queda acumulado como nuevo capital y genera más intereses. Eso nos permite ganar más dinero que con el interés simple.
Como ya hemos explicado en clase el capital final depositado en un banco después de n años es
se puede considerar como una progresión geométrica de primer término Co, y de razón (1+ r), siendo r el porcentaje de interés que da el banco anualmente, expresado en decimal, elevado a los años que dejas el capital ingresado en el banco.

En el caso de un capítulo de Futurama, Fry (que estuvo congelado 1000 años), va a su antiguo banco para ver cuánto dinero tiene para pagar una multa. Tenía 93 centavos, 0.93 $, pero después de 1000 años este capital ridículo se transforma en 4300 millones de dólares. Es decir, 0.93 $ a un interés de 2,25 %, durante mil años da un capital final Cf = 0.93· (1 + 0.0225) elevado a 1000 = 4.283.508.449,71 $.
Como ya hemos explicado en clase el capital final depositado en un banco después de n años es
se puede considerar como una progresión geométrica de primer término Co, y de razón (1+ r), siendo r el porcentaje de interés que da el banco anualmente, expresado en decimal, elevado a los años que dejas el capital ingresado en el banco.
En el caso de un capítulo de Futurama, Fry (que estuvo congelado 1000 años), va a su antiguo banco para ver cuánto dinero tiene para pagar una multa. Tenía 93 centavos, 0.93 $, pero después de 1000 años este capital ridículo se transforma en 4300 millones de dólares. Es decir, 0.93 $ a un interés de 2,25 %, durante mil años da un capital final Cf = 0.93· (1 + 0.0225) elevado a 1000 = 4.283.508.449,71 $.
lunes, 18 de noviembre de 2019
SUCESIONES Y PROGRESIONES

hola, os ponemos una ficha de sucesiones y progresiones aritméticas y geométricas para practicar. Pinchad en el siguiente enlace. SUCESIONES Y PROGRESIONES
Suscribirse a:
Comentarios (Atom)