an+2 = a n+1 +a n
La sucesión más antigua y más conocida es la sucesión de Fibonacci, A={0. 1. 1. 2. 3. 5. 8. 13. 21. ...}, que conlleva un problema planteado por Fibonacci. El problema dice así: ¿Cuántas parejas de conejos tendremos a fin de año, si comenzamos con una pareja que produce cada mes otra pareja que procrea a su vez a los dos meses de vida?

Tras un número muy grande de términos, el cociente entre el último y el penúltimo término tiende a un número irracional llamado Razón áurea
Es un número especial que se encuentra al dividir una línea en dos partes, de modo que la parte más larga (a) dividida por la parte más pequeña (b) es igual a la longitud total dividida por la parte más larga.
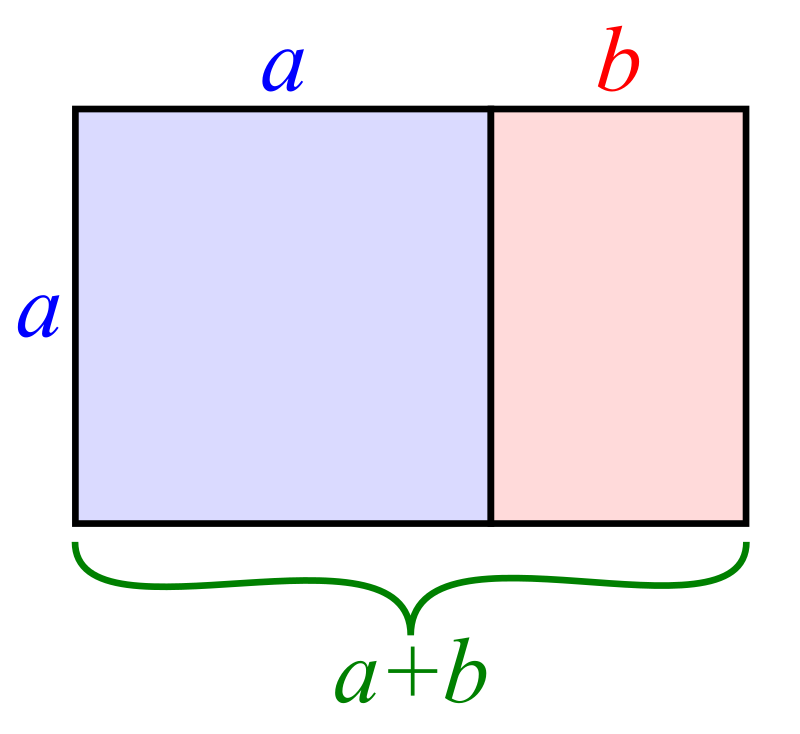

Eso dio lugar a crear con esas dimensiones rectángulos armoniosos, presentes en muchas obras de arte y en muchas medidas en la naturaleza (por ejemplo relaciones entre partes consecutivas del cuerpo humano, etc...),
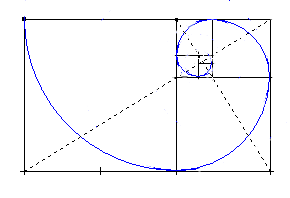
Los números de la sucesión de Fibonacci consiguen crear en cada paso un rectángulo áureo.
Además si creamos con arcos de circunferencia con los rectángulos formados obtenemos una espiral áurea, también presente en muchos aspectos de la naturaleza.
El trabajo de investigación que tenéis que hacer es encontrar 1 ejemplo de la naturaleza o el arte donde se recreen estos números de Fibonacci, o las razones áureas o rectángulos áureos o espirales áureas. Buscáis imágenes que lo muestren y lo guardáis en un archivo de texto con vuestro nombre y apellidos, el curso donde estáis, añadiendo la palabra Fibonacci y lo mandáis al siguiente correo
matesinstitutolamanga@gmail.com
Este trabajo es independiente de los exámenes y es una nota que se suma a la nota final de curso con un peso de 0.2 %, o sea 0.02 puntos a añadir a la nota final. Esperamos vuestros trabajos de investigación. Fecha límite 13 de diciembre de 2019
No hay comentarios:
Publicar un comentario